Multi-Stage Monte Carlo Optimization
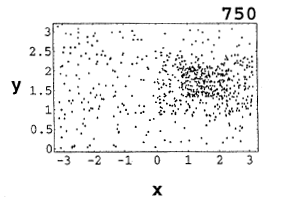
Monte Carlo optimization has been a widely used optimization method for many years. It’s very easy to understand: For a set of factors (independent variables), randomly select values for each factor to make a set of inputs to the system and test the system response for each set. For example, referring to the picture, we would pick different (x,y) value pairs and test the system response.
Monte Carlo optimization has several advantages:
- It will not be distracted by high variability in the system response since it doesn’t care what the response is.
- You do not need to have much of an understanding of the system response. You just define the range of values for each input and let the method randomly pick test sets.
Monte Carlo optimization also has several disadvantages:
- The method does not learn from test results as it runs. An area where the optimum probably is located may become clear after a certain number of tests but the method won’t know it and will just blindly keep testing random points.
- You often need a large sample size of points to find the optimum, and if each test is expensive (e.g., an airplane flight test or a complex manufacturing process) then the costs of using Monte Carlo would be prohibitive.
What would improve the method is a way to break up the sampling so that more points could be run in the area where the optimum value is more likely to be. This is what Multi-Stage Monte Carlo does, and I modified the method to adjust the sampling to handle cases where there are many local optima in the response surface. Today Monte Carlo optimization is not used as widely as before but there are times when it’s still the best method, and the Multi-Stage and Enhanced Multi-Stage algorithms can help to lessen some of the disadvantages.
Multi-Stage Monte Carlo Optimization Presentation (scanned pdf)